Dijkstra’s algorithm
To be frank, I hate mathematics, due to the nature of my work now, I got to use all this skillsets. For the last few weeks, I’d been studying a new algorithm to make one of my apps more intelligent, as for the finding, I write this article to explain a simple but powerful algorithm : Dijkstra’s algorithm.
Dijkstra’s algorithm can be describe as the father of all modern GPS routing engine. Without it, we will have hard time to figure out which is the best route (regardless fastest in time, shortest in distance) to use to reach our destination.
Dijkstra’s algorithm is named after Dutch computer scientist Edsger W. Dijkstra. The objective of this algorithm is to find the shortest path between two given nodes. Dijkstra’s algorithm does exist in various variants, regardless what variants is it, the basic of these algorithm are the same.
The algorithm
Let the node that we are going to start with called the initial node.
Let the distance of node Y be the distance from the initial node to Y. Dijkstra’s algorithm will assign some initial distance values and will try to improve them step by step.
- Assign to every node a tentative distance value: set it to zero for our initial node and to infinity for all other nodes.
- Set the initial node as current. Mark all other nodes unvisited. Create a set of all the unvisited nodes called the unvisited set.
- For the current node, consider all of its unvisited neighbors and calculate their tentative distances. Compare the newly calculated tentative distance to the current assigned value and assign the smaller one. For example, if the current node A is marked with a distance of 6, and the edge connecting it with a neighbor B has length 2, then the distance to B (through A) will be 6 + 2 = 8. If B was previously marked with a distance greater than 8 then change it to 8. Otherwise, keep the current value.
- When we are done considering all of the neighbors of the current node, mark the current node as visited and remove it from the unvisited set. A visited node will never be checked again.
- If the destination node has been marked visited (when planning a route between two specific nodes) or if the smallest tentative distance among the nodes in the unvisited set is infinity (when planning a complete traversal; occurs when there is no connection between the initial node and remaining unvisited nodes), then stop. The algorithm has finished.
- Otherwise, select the unvisited node that is marked with the smallest tentative distance, set it as the new “current node“, and go back to step 3.
Example
Let see the above teaching in action.
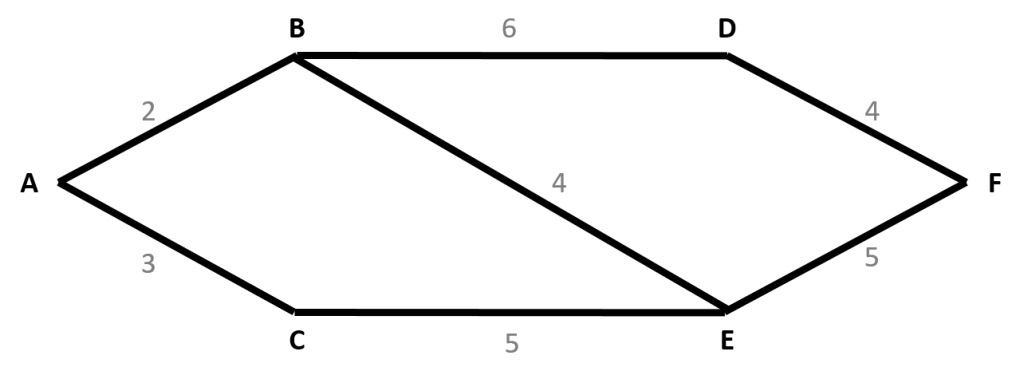
We are going to find the shortest path from A to F, using the following graph.
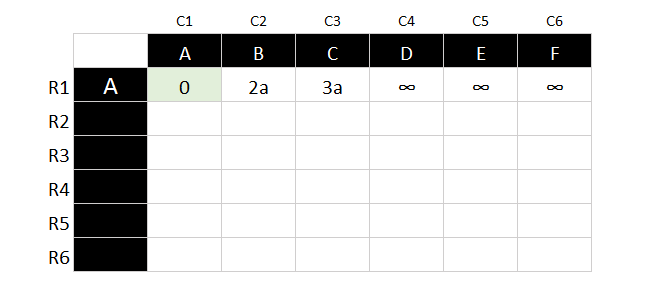
- First of all we open an Excel Worksheet, and assign put down all the possible nodes in one row.
- Since we are going to start from point A, we assign value for the first row as A and the value of A to A is 0 and the calculate the value for all the connected nodes, assign infinity(∞) for the rest. We also put a lower cap of the letter to indicate this value is calculated based on coming from which note. Just like the chart below.
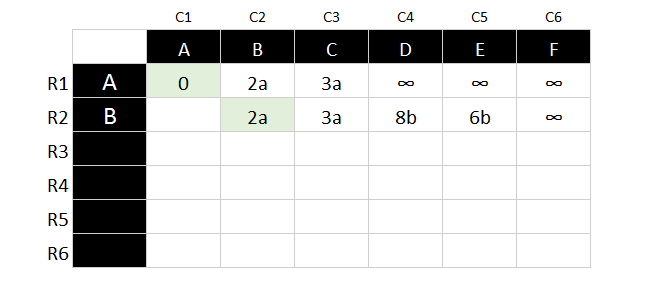
- Copy the smallest value to next row, and assign repeat the calculation of the new node to the rest of the connected node. Node B is not connected to C, so we are just copied the calculated value over.
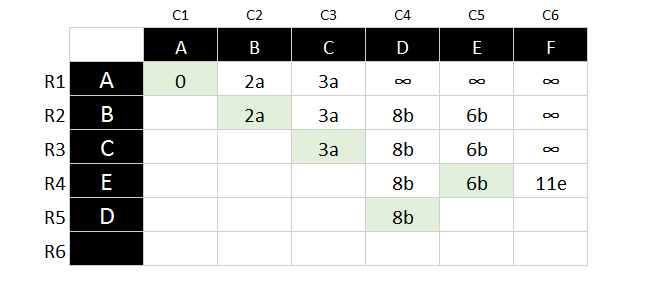
- Repeat the above process until you find all the values for each nodes.
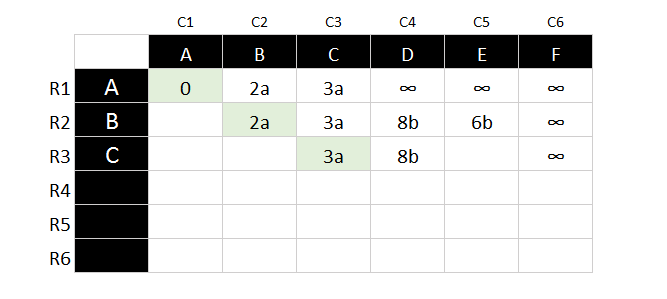
- If we calculate the value for node C to node E, the value will be 8 which is bigger than 6 which we had calculated early. Hence, we will not accept the new value but kept the original value.
- This is the result for all the nodes which start from node A. If you would like to find out the initial node to other node, you will have to repeat the above process.
How to read the chart?
For example, if you want to find out the shortest path from A to F, we start reading from F. At row R4, node F, it said 11e; this mean to reach F is from node E, we follow path to find E value, which is 6b, from 6b it bring us to 2a and finally it lead us to 0a.
Now we can establish the path, F – E – B – A, by reversed the sequence, we knew the shortest path from node A to F is A – B – E – F.
On the next article, I will put this Dijkstra’s algorithm into C# code, and to demonstrate more complicated calculation.